Fibonacci Resistor Network

Recently at work, I needed to determine the impact of removing some top-level power supply routing from a circuit. Out of curiosity, I decided to see if there was a way to have an expression for an arbitrary number of routes at arbitrary resistances (the answer is no, as it turns out) but an interesting result came out of it.

Framing the Problem

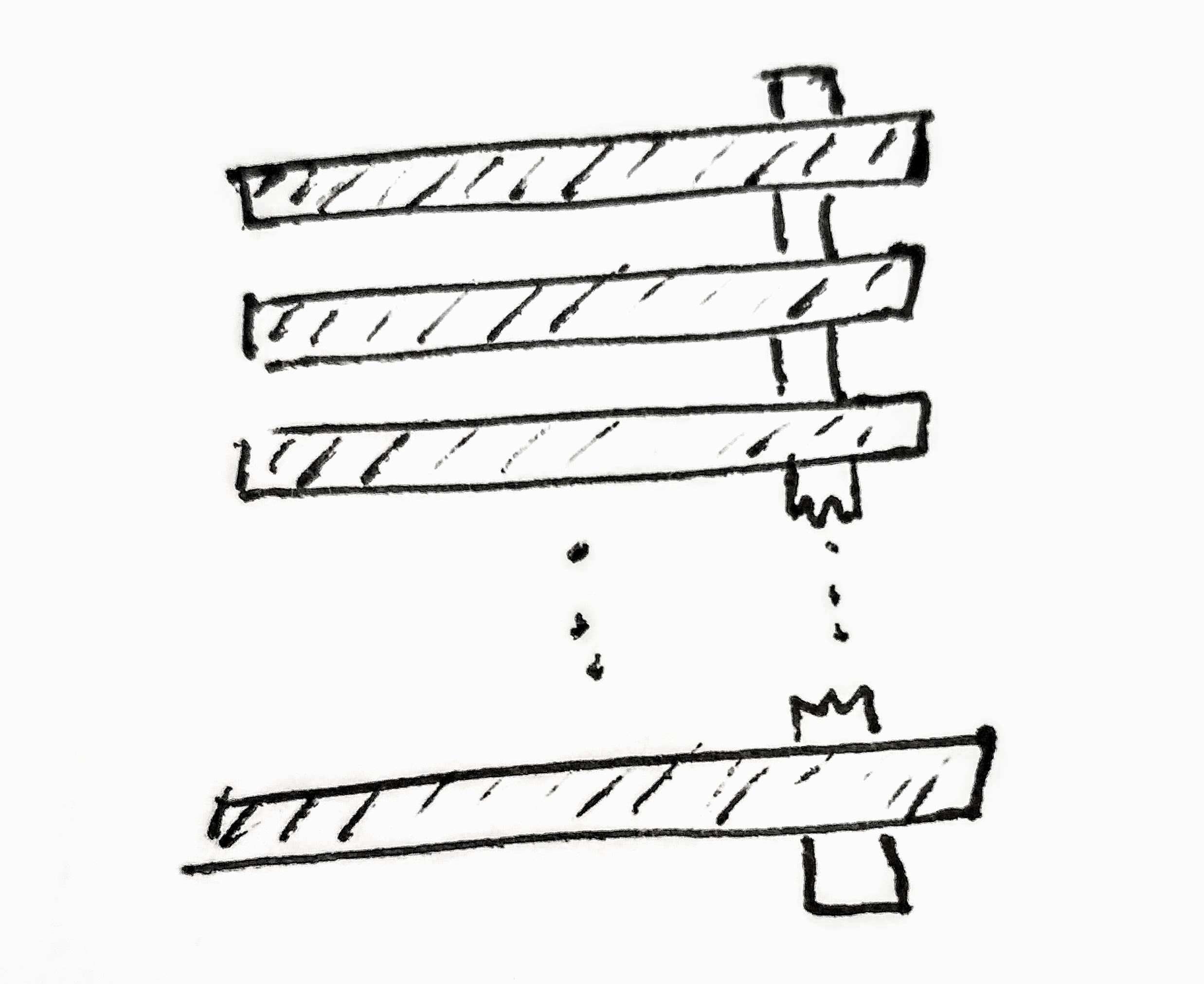
So to take a step back, imagine the following scenario: A circuit with a constant current draw has multiple pieces of metal routed on top of it in a left-to-right fashion. Theses routes begin at the top of the circuit and there are ‘N’ number of them, evenly spaced, as you progress from top-to-bottom. These metal routes then connect down to vertical metal routes that extend all the way up to the constant current circuit. To visualize this metal grid, refer to the following image.

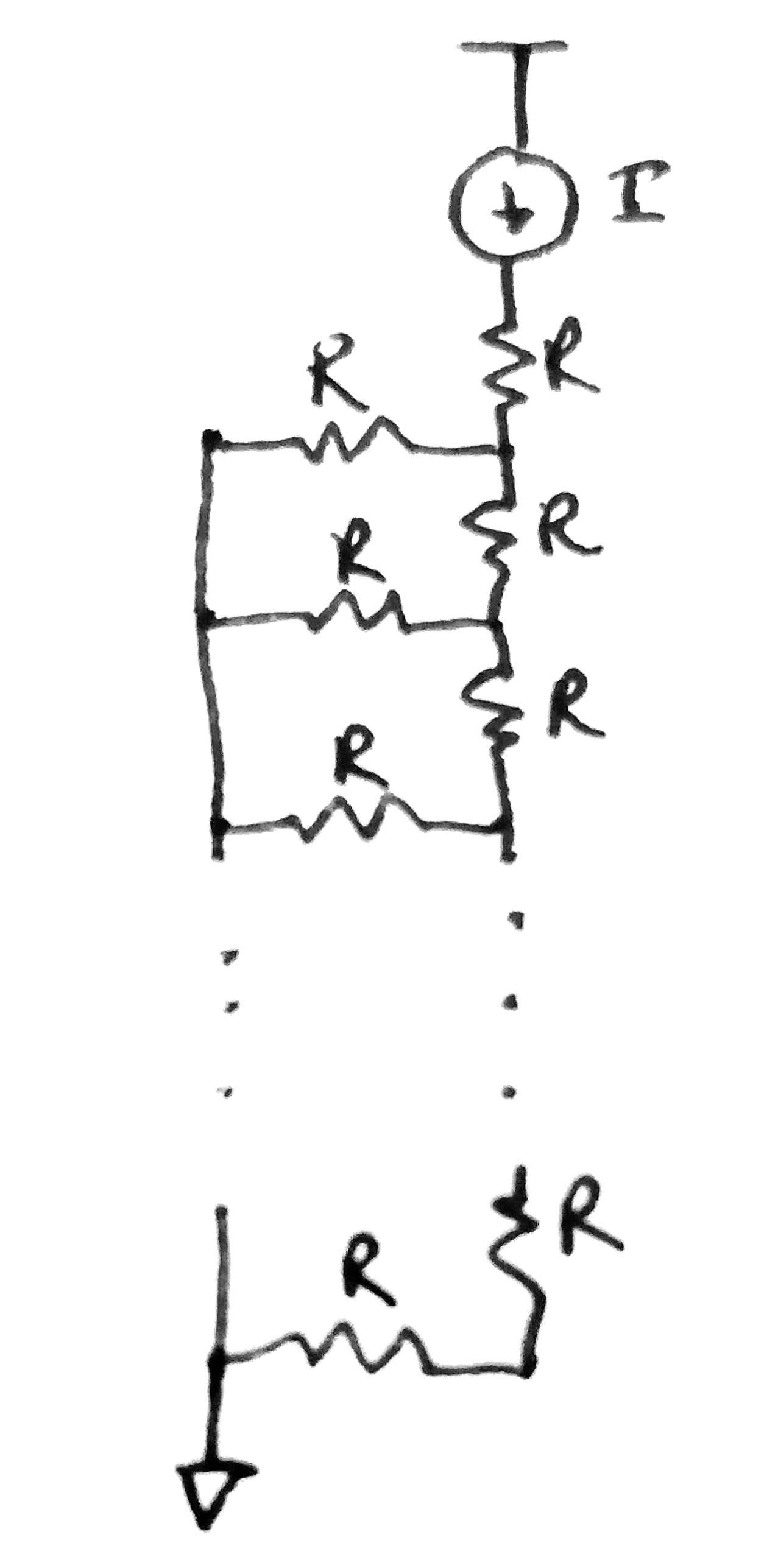
So to reiterate, the circuit sees ‘N’ number of resistors to the supply (let’s just say it’s ground) through ‘N’ number of series resistors connected in between these routes.

If we take that information, we can create a circuit model to solve the problem. The interesting thing happens when we make all of theses resistances equal to ‘R’ (ie. they’re all the same resistance).

Solving the Problem

To solve this, I took the approach of solving for N=1, N=2, etc. in order to find a pattern that would create a general solution.

N = 1

Here we have $R_{eq} = R + R = 2R$

N = 2

Now we see this previous solution in parallel with a single $R$ and that parallel combination in series with a single $R$. At this point it is possible to create a solution that says $R_{eq}(N) = R + R_{eq}(N-1)||R$. But this doesn’t create our interesting solution… so we will continue on with plugging in numbers:

N = 3

++R_{eq} = R + \frac{5}{3}R||R = R + \frac{5}{8}R = \frac{13}{8}R++

N = 4

++R_{eq} = R + \frac{13}{8}R||R = R + \frac{13}{21}R = \frac{34}{21}R++

Wait a minute…

It was at this point that I noticed a trend. If you split each solution into denominator and then numerator of the first solution followed by the denominator and numerator of the next solution, and so forth the series ${3, 5, 8, 13, 21, 34}$ appears which is a subset of the well-known Fibonacci Sequence. Specifically, the denominator is the $2N^{th}$ number in the sequence and the numerator is the $(2N+1)^{th}$ number in the sequence. Thus, our actual solution is:

++R_{eq} = \frac{F_{2N+1}}{F_{2N}}R++

which, to me, is cool as hell. This solution had no bearing on what I originally set out to find, but was just a really cool side result that I felt was worth sharing. The Fibonacci Resistor Network, everyone!